A second new paper: "A fiscal theory of monetary policy with partially repaid long-term debt."
By "fiscal theory of monetary policy" I mean a model with standard DSGE ingredients, including inertemporal optimization and market clearing, monetary policy described by interest rate targets, price or other frictions, but closed by fiscal theory, "active" fiscal policy rather than "active" monetary policy.
I aim to build a standard simple but somewhat realistic model of this sort, a parallel to the three equation textbook model that has been part of the new-Keynesian tool kit since the 1990s. I keep the model as simple and standard as possible, so the effect of the innovations one the fiscal side are clearer.
Two parts of the specification are central. First, long-term debt allows the model to produce a negative response of inflation to interest rates. Long-term debt also allows a fiscal shock to result in a protracted inflation, which slowly devalues long term bonds, rather than a price level jump.
Second, and most important, the paper writes down a process for fiscal surpluses in which today's deficits are partially repaid by tomorrow's surpluses. Look quickly at the surplus response functions in my last post. When the government runs a deficit, it reliably runs subsequent surpluses that partially repay some of the accumulated debt. The surplus is not an AR(1)! It has an s-shaped response function.
So if you want a realistic fiscal theory model, you need a surplus with an s-shaped response function, but you need to keep "active" fiscal policy. This combination is the central innovation of the paper.
Active and passive
As a quick reminder for new readers, here's what active and passive mean. Take a really simple model with flexible prices, one period debt, a constant zero real rate, and an interest rate target. The economic model boils down to just $$ i_{t} = E_t \pi_{t+1} $$ $$ \Delta E_{t+1} \pi_{t+1} = \Delta E_{t+1} \sum_{j=0}^\infty \rho^j s_{t+1+j}. $$ \(i\) is the nominal interest rate, \(\pi\) is inflation, \(s\) is real primary surplus, and the linearization is is derived in my last post. Unexpected inflation or deflation changes the value government debt, which must equal the present value of surpluses.
The central bank, by setting the interest rate target, determines expected inflation. But unexpected inflation is not then determined. If fiscal policy is "active" the second equation and the revision to expected surpluses determines unexpected inflation. If fiscal policy is "passive" meaning that the surplus process reacts to unexpected inflation so that the second equation hold for any value of unexpected inflation, then we need another model equation, "active" monetary policy, to determine unexpected inflation.
My goal is to create a model like this, but with sticky prices and output and real interest rate variation, with an empirically sensible specification of surplus (fiscal) policy, that is nonetheless "active" and so closes out the model, determining unexpected inflation.
AR(1) puzzles
So far, many fiscal theory puzzles have come from assuming an AR(1) or similar positively autocorrelated surplus process. An s-shaped surplus process solves the puzzles -- and, conversely, the puzzles provide many different pieces of evidence that the AR(1) is a terrible assumption.
Puzzle 1. Deficits and inflation. An AR(1) surplus predicts that deficits come with substantial inflation. By and large we see the opposite sign, less inflation with deficits in a recession and vice versa, and little reliable correlation. An s-shaped surplus process solves the puzzle.
I'll illustrate with a constant interest rate, short term debt version of the model. The simple FTPL is$$ \frac{B_{t-1}}{P_t} = E_t \sum_{j=0}^\infty \beta^j s_{t+j} = \frac{1}{1-\beta\rho_s} s_t$$ where \(B\) is nominal debt, \(P\) is price level and \(s\) is real primary surplus and the last term uses an AR(1). Manipulating, $$ \frac{B_{t-1}}{P_{t-1}} \Delta E_t \left( \frac{P_{t-1}}{P_t} \right) = \Delta E_t \sum_{j=0}^\infty \beta^j s_{t+j}=\frac{1}{1-\beta\rho_s}\varepsilon_{s,t}$$ where \(\Delta E_t \equiv E_t - E_{t-1}\). A positive shock to surpluses is a negative shock to inflation, and a deficit means inflation. Since \(1/(1-\beta\rho_s)>1\) inflation is also very volatile.
How can we cure this puzzle? Well, the key assumption is that a shock to surpluses today raises forecasts of surpluses in the future -- all the \(s_{t+j}\) terms are positive. Suppose that the surplus process looks like the graphs in my last post -- in that case that a deficit today (negative \(s_t\)) implies a long string of positive future \(s_{t+j}\) terms that bring the sum back, perhaps all the way to zero. If the sum of future surpluses is a small number, this force for deficits with inflation can be overwhelmed by other forces.
Puzzle 2: Damningly, the AR(1) or other positively autocorrelated surplus predicts that a higher surplus todayraises the value of the debt tomorrow, just as a higher dividend today leads to a higher stock price. A higher surplus forecasts higher future surpluses, and the value of the debt is the present value of subsequent surpluses. Yet higher surpluses in the data unequivocally pay down the value of the debt, and deficits result in more debt, as pointed out by Canzoneri, Cumby and Diba.
A surplus process with an s-shaped moving average solves the puzzle. A higher surplus today corresponds to a decrease in present value of subsequent surpluses, and hence a decline in the value of debt.
Puzzle 3: With AR(1) or positively autocorrelated surpluses, all deficits are paid for by devaluing outstanding debt via inflation (or default), and none are paid for by selling new debt. Running a deficit involves selling less real debt. With an s-shaped moving average, deficits are financed by borrowing.
Bond buyers will only hand over resources to finance today's deficits if they are convinced that the bonds will be paid off by future surpluses, essentially proving that bond buyers think the surplus process is s-shaped.
Puzzle 4: Models with positively autocorrelated surpluses predict that the risk and hence expected return of government bonds should be huge. The s-shaped surplus process solves this puzzle, allowing even risk free government debt.
Since all deficits are paid by unexpectedly inflating away bonds, since \(1/(1-\beta \rho_s)\) is a large number, the AR(1) predicts lots of inflation and hence lots of volatility in real ex-post bond returns. As above the inflation and negative bond returns come in recessions, so that volatility should generate a large risk premium. Equivalently, looking at the present value formula, the surplus is volatile and procyclical, like dividends. So bond returns should be volatile and procyclical, like stocks, and carry an equity premium. Actual government bond returns are quiet (low volatility), countercyclical (they do well in recessions) and carry a very low mean. Jiang, Lustig, Van Nieuwerburgh, and Xiaolan point out this puzzle.
An s-shaped surplus process resolves the puzzle. When the ``dividend,'' surplus, falls, the ``price,''
present value of subsequent surpluses, rises. The overall return need not move at all, nor offer a positive compensation for risk. Stock dividends don't follow an s-shaped process. Government deficits and surpluses do.
The standard specification of fiscal policy is $$s_t = \gamma v_t + u_{s,t}$$$$u_{s,t}=\rho_s u_{s,t-1} + \varepsilon_{s,t}$$ where \(v\) is the real value of the debt. If we set \(\gamma=0\) then we have all the AR(1) puzzles. If we set \(\gamma>0\) then we have an s-shaped response, in fact the response of the discounted sum of future surpluses is zero. But then fiscal policy is passive. It has seemed we are stuck, and the puzzles tell us fiscal policy must be passive. But wait, who said the \(u\) process has to be an AR(1)? By abandoning that auxiliary assumption, I create a model with \(\gamma=0\) and active fiscal policy that also solves the puzzles and fits the s-shaped estimates of the surplus process. A regression of model data will show \(\gamma>0\) though that is a mis specified regression and the true \(\gamma=0\).
The model
OK, hold your breath. Here is the model. If this is too much in one bite, read the paper which builds up to the model bit by bit. (The whole point of this blog post is to get you to read the paper after all!) Here we'll just sit down to the main course without appetizers.
\begin{align}
x_{t} & = E_{t}x_{t+1}-\sigma(i_{t}-E_{t}\pi_{t+1})\label{IS}\\
\pi_{t} & =\beta E_{t}\pi_{t+1}+\kappa x_{t} \label{NK}\\
i_{t} & =\theta_{i\pi}\pi_{t}+\theta_{ix}x_{t}+u_{i,t}\label{nm4}\\
s_{t} & =\theta_{s\pi}\pi_{t}+\theta_{sx}x_{t}+\alpha v_{t}^{\ast}+u_{s,t}%
\label{nm5}\\
\eta v_{t+1}^{\ast} & =v_{t}^{\ast}+i_{t}-E_{t}\pi_{t+1}-s_{t+1}%
\label{nm6}\\
\rho v_{t+1} & =v_{t}+r_{t+1}^{n}-\pi_{t+1}-s_{t+1}\label{nm7}\\
E_{t}r_{t+1}^{n} & =i_{t}\label{nm8}\\
r_{t+1}^{n} & =\omega q_{t+1}-q_{t}\label{nm9}\\
u_{i,t+1} & =\rho_{i}u_{i,t}+\varepsilon_{i,t+1}\label{nm10}\\
u_{s,t+1} & =\rho_{s}u_{s,t}+\varepsilon_{s,t+1}. \label{nm11}%
\end{align}
The first two equations are the standard intertemporal substitution (IS) and forward-looking Phillips curve. The third equation is a standard interest rate policy rule.
The surplus \(s\) equation also starts with a policy rule. Surpluses rise with output, a very strong correlation in the data, and potentially also with inflation. Now for the fun part: Surpluses respond to the state variable \(v^\ast\) but not to the value of debt itself, so fiscal policy remains active. The state variable \(v^\ast\) accumulates past deficits, and responds to change in expected return of government bonds, but crucially it does not respond to ex-post returns induced by unexpected inflation. The actual value of debt \(v\) follows a similar process, but it does respond to ex-post returns induced by unexpected inflation.
One way to think of the difference between \(v^\ast\) and \(v\) is that the government makes a distinction: It will respond with greater surpluses to higher debts that come from its own borrowing and higher real interest rates. But it will not respond with greater surpluses to a higher real value of debt that comes from an unexpected, unintended, or multiple-equilibrium inflation. The key to "active" fiscal policy is only the last point -- an "active" fiscal policy can respond to any other source of debt variation. The paper goes on (and on) to argue that this is quite sensible and a good reading of many institutions and historical episodes. Including 2008. Why was there not deflation? Because if there was a huge deflation, as standard Keynesian models (new and old) predicted, then the real value of debt would have had to soar. Had a big deflation occurred in 2008, as feared, would Congress really have "passively" raised taxes and slashed spending in order to fund an unexpected and, surely it would be argued, undeserved windfall payment to fat-cat Wall Street bankers and the Chinese central bank? Without that action the deflation cannot happen. Similarly, take a look at Jacobson, Leeper and Preston's marvelous analysis of 1933, when the US again refused to validate a deflation. You can also think of \(v^\ast\) as just a latent variable that represents an s-shaped moving average in vector AR(1) form, of course.
The parameter \(\eta\) adjusts how much debt gets repaid. If \(\eta=\rho\) then all debt is repaid, the right end of the s pays off the initial deficits completely, and the response of \(\sum s_{t+j}\) to a shock is zero. We want to allow for some fiscal inflation, however -- fiscal policy responds to a shock by partially inflating away existing debt, and partially by borrowing and promising future surpluses. \(\eta>\rho\) allows that. \(\eta \rightarrow \infty\) recovers a pure AR(1) surplus shock.
The \(v\) equation is the evolution of the real value of government debt in linearized form. \(r^n\) is the nominal ex-post return on the government bond portfolio, so includes long-term debt. The \(r^n\) equation is the expectations hypothesis. We need a bond pricing formula, and I kept it simple along with everything else not fiscal. The \(r^n\) equation is the return on the government bond portfolio in terms of its price \(q\). The last equations are AR(1) shocks to monetary and fiscal policy.
Responses
Here are the responses to a fiscal policy shock, a unit \(\varepsilon_{s,1}\) with no movement \(\varepsilon_{i,1}\) and thus no movement in the monetary policy disturbance \(u_i\). Monetary policy may still react via inflation and output. I picked parameters to make the plots look pretty, see the paper.
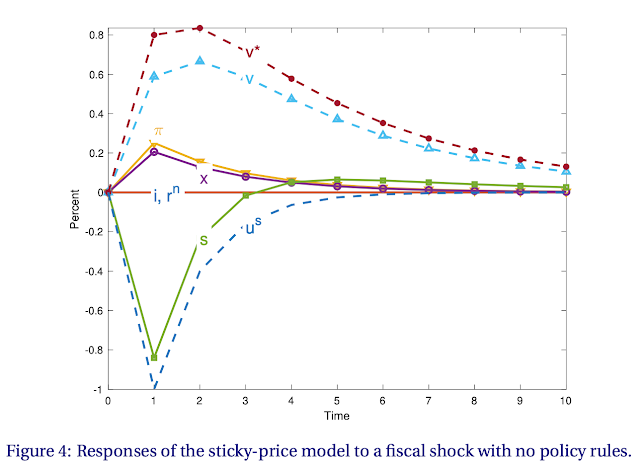
This first response has no policy rules -- the \(\theta\) terms are turned off -- so you can see how the model behaves. The surplus does have an s shaped response, not an AR(1). But it would be darn hard to tell from the AR(1) disturbance \(u^s\). Similarly, the state variable \(v^\ast\) and actual debt \(v\) are similar. The surplus will seem to respond to \(v\) and policy will seem passive if you're not really careful. The initial deficits lead to a rise in debt, which is then slowly paid down by a small string of surpluses.
The fiscal shock leads to a AR(1) pattern of inflation, and as a consequence of the standard Phillips curve an output expansion. With no policy response, interest rates stay put. Now, let's add a monetary and fiscal policy response.
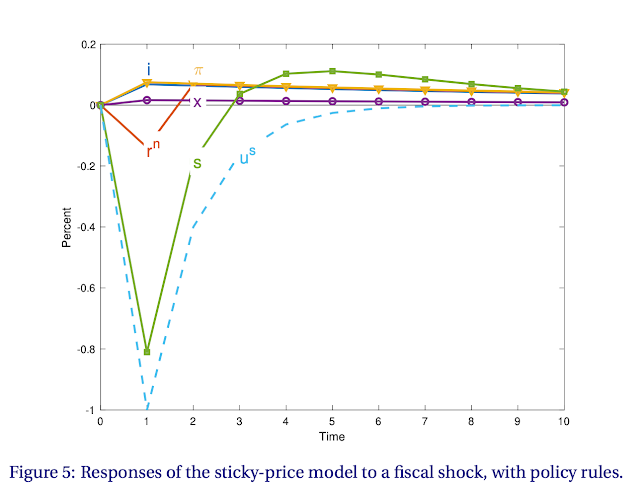
The rise in inflation and output provokes a rise in interest rate. And the initial inflation devalues long term bonds \(r^n\). Together, monetary policy and long term debt substantially reduce the inflationary impact of the fiscal shock and draw it out. The larger output also gives rise to larger surpluses, which reduces the size of the fiscal shock to begin with.
Big points: 1) Fiscal theory does not just imply big price level jumps in response to fiscal shocks. Fiscal theory rather naturally here leads to a very long and drawn out inflation in response to a fiscal shock. 2) Endogenous monetary and fiscal policy responses also draw out and buffer the response to a fiscal shock.

Here is the response to a monetary policy shock \(\varepsilon_{m,1}\) holding constant the fiscal policy shock \(\varepsilon_{s,1}\), with no policy rule responses \(\theta=0\). The interest rate and its shock follow an AR(1). Output and inflation decline persistently. Whether true or not in the data, this is the sort of response that is the Holy Grail of monetary theory. At least the model can produce this result.
Surpluses are not constant, because they react to the rise in value of debt that comes from higher real interest rates, represented by the difference between the interest rate and inflation lines. Bond returns follow the expectations hypothesis, mirroring the interest rate with a one period lag, except in the first period. A rise in interest rates leads to a big ex-post decline in bond prices.
Last and most of all, here is the response to monetary policy with policy rules in place.

There is a lot more going on here. Real interest rate variation leads to discount rate effects, for example. But I what to whet your appetite to read the paper.
The goal: a really simple baseline fiscal theory of monetary policy model that produces reasonable responses to fiscal and monetary policy. We have drawn out inflation in response to fiscal shocks, not a price level jump; we have lower inflation and output in response to monetary policy not instant Fisherism; and all the AR(1) puzzles are solved. It seems a good place to start. And, for today, to stop.
(Note: this post uses Mathjax to display equations, which is not working perfectly.)





